BSIT
布里渊诱导透明
参数介绍
腔内有两个光学模式:$\omega_1$,$\omega_2$
腔内有一个布里渊模式:$\Omega_m$
在$\omega_1$附近的强控制光:$\omega_c$
在$\omega_2$附近的弱泵浦光:$\omega_p$
各失谐量:
$\Delta_1=\omega_c-\omega_1$
$\Delta_2=\omega_p-\omega_2$
$\delta=\omega_2-\omega_1-\Omega_m$
$\Delta_B=\omega_p-\omega_c-\Omega_m$
哈密顿量
未经过布里渊耦合时:
$$
\begin{aligned}
H&=\hbar\omega_1 a^\dagger_1 a_1+\hbar\omega_2 a^\dagger_2 a_2\\
&+i\hbar\sqrt{\kappa_{ex,1}}s_{in,1}(a^\dagger_1 e^{-i\omega_c t}-a_1 e^{i\omega_c t})\\
&+i\hbar\sqrt{\kappa_{ex,2}}s_{in,2}(a^\dagger_2 e^{-i\omega_p t}-a_2 e^{i\omega_p t})
\end{aligned}
$$
那么以$\omega_c$光为参考,即选择酉变换$U=\exp(i\omega_c a^\dagger_1 a_1 t)$,此时模式一的运动方程为(考虑了损耗)
$$\frac{da_1}{dt}=i\Delta_1 a_1-\frac{\kappa_1}{2}a_1+\sqrt{\kappa_{ex,1}}s_{in,1}$$
这里用到公式$H’=U H U^\dagger -i\hbar U\partial U^\dagger /\partial t$
在稳态是,导数为零,我们解得
$$a_1=\frac{\sqrt{\kappa_{ex,1}}s_{in,1}}{-i\Delta_1+\kappa_1/2}$$
在实验室参考系中,应该在做逆变换
$$U a_1 U^\dagger=\frac{\sqrt{\kappa_{ex,1}}s_{in,1}}{-i\Delta_1+\kappa_1/2}e^{-i\omega_ct}$$
当经过布里渊耦合时,哈密顿量为
$$
\begin{aligned}
H&=\hbar\omega_1 a^\dagger_1 a_1+\hbar\omega_2 a^\dagger_2 a_2+\hbar\Omega_m b^\dagger b+\hbar g(a^\dagger_1 b^\dagger a_2+a_1 b a^\dagger_2)\\
&+i\hbar\sqrt{\kappa_{ex,1}}s_{in,1}(a^\dagger_1 e^{-i\omega_c t}-a_1 e^{i\omega_c t})\\
&+i\hbar\sqrt{\kappa_{ex,2}}s_{in,2}(a^\dagger_2 e^{-i\omega_p t}-a_2 e^{i\omega_p t})
\end{aligned}
$$
由于控制光为强光,那么我们可以认定$a_1$为一复数,$a_1^\dagger a_1=n_1$,所以
$$a_1=\sqrt{n_1}e^{-i\omega_c t}=\left|\frac{\sqrt{\kappa_{ex,1}}s_{in,1}}{-i\Delta_1+\kappa_1/2}\right|e^{-i\omega_c t}$$
将其代入哈密顿量,并忽略常数项,我们得到
$$
\begin{aligned}
H&=\hbar\omega_2 a^\dagger_2 a_2+\hbar\Omega_m b^\dagger b+\hbar g\sqrt{n_1}(b^\dagger a_2 e^{i\omega_c t}+b a_2^\dagger e^{-i\omega_c t})\\
&+i\hbar\sqrt{\kappa_{ex,2}}s_{in,2}(a^\dagger_2 e^{-i\omega_p t}-a_2 e^{i\omega_p t})
\end{aligned}$$
对于上述的哈密顿量,我们选择酉变换$$U=\exp(i\omega_p a^\dagger_2 a_2 t+i(\omega_p-\omega_c)b^\dagger b t)$$
我们得到变换后的哈密顿量为
$$
\begin{aligned}
H&=\hbar(\omega_2-\omega_p)a^\dagger_2 a_2+\hbar(\Omega_m-(\omega_p-\omega_c))b^\dagger b\\
&+\hbar g\sqrt{n_1}(b^\dagger a_2 +b a^\dagger_2)+i\hbar\sqrt{\kappa_{ex,2}}s_{in,2}(a^\dagger_2-a_2)\\
&=-\hbar \Delta_2 a^\dagger_2 a_2-\hbar \Delta_B b^\dagger b\\
&+\hbar g\sqrt{n_1}(b^\dagger a_2 +b a^\dagger_2)+i\hbar\sqrt{\kappa_{ex,2}}s_{in,2}(a^\dagger_2-a_2)\\
\end{aligned}$$
得到哈密顿量后我们可以写出泵浦光和布里渊模的运动方程(考虑损耗)
$$
\begin{array}{}
\frac{da_2}{dt}=(i\Delta_2-\kappa_2/2) a_2-ig\sqrt{n_1}b+\sqrt{\kappa_{ex,2}}s_{in,2}\\
\\
\frac{db}{dt}=(i\Delta_B-\Gamma_m )b-i g \sqrt{n_1}a_2
\end{array}
$$
在稳态下求解的,
$$
a_2=-\frac{\sqrt{\kappa _{\text{ex},2}} s_{\text{in},2}}{\frac{g^2 n_1}{-\Gamma _m+i \Delta _B}+i \Delta _2-\frac{\kappa _2}{2}}
$$
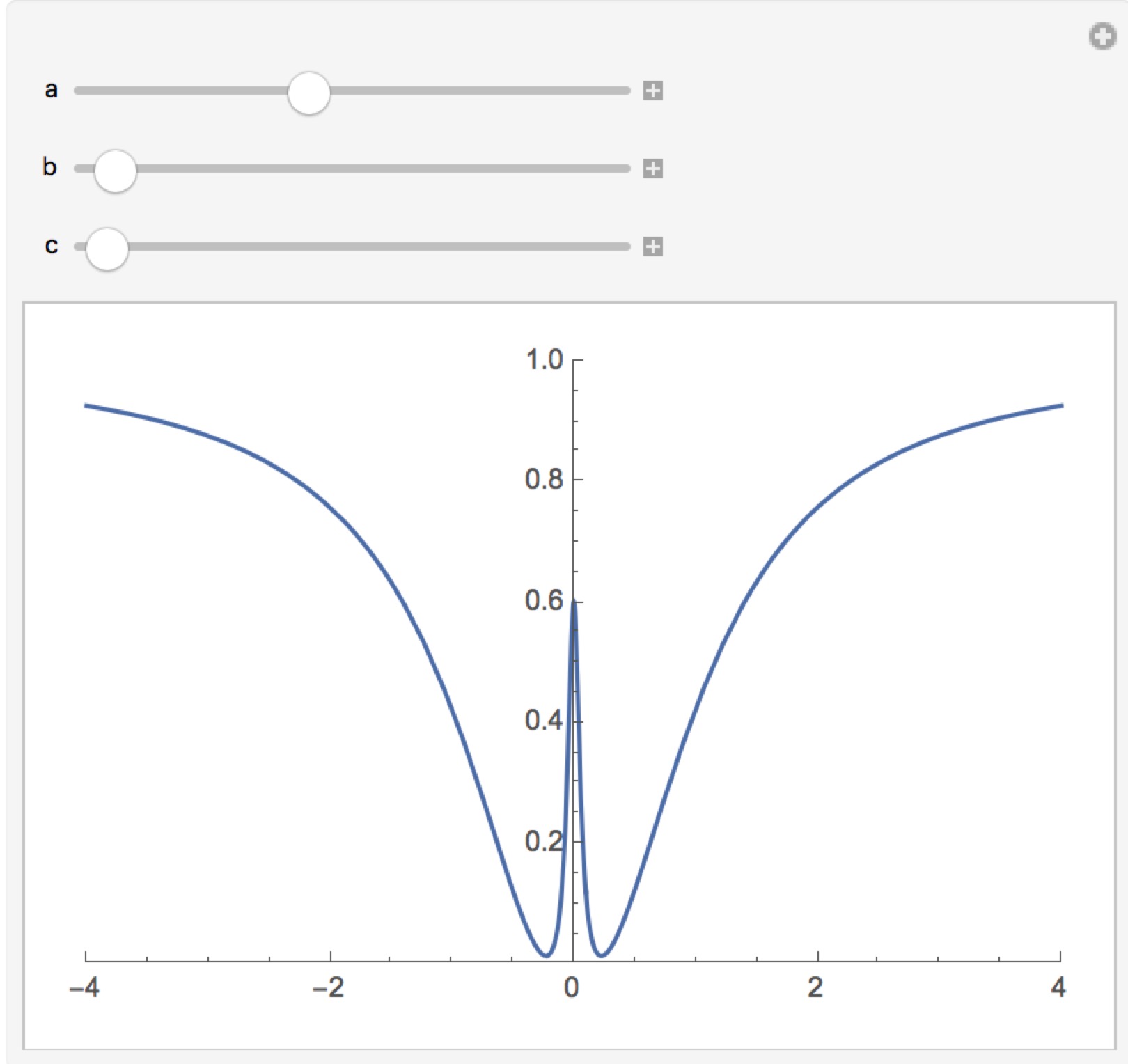
代入输入输出关系$s_{out,2}=s_{in,2}-\sqrt{\kappa_{ex,2}}a_2$,求出投射谱
$$T=\text{Abs}\left(1-\frac{\sqrt{\kappa_{ex,2}}a_2}{s_{in,2}}\right)^2$$Mathematica代码如下