郎之万方程
理论分析
布朗粒子在液体中会受到液体分子的随机碰撞而产生随机运动,以一维粒子为例
$$
\begin{aligned}
m\frac{dv}{dt}&=K(t)\\
&=-\gamma_0v+F_0(t)
\end{aligned}
$$
其中$-\gamma_0v$是与速度相关的摩擦力,$F_0(t)$是粒子收到碰撞的随机力,其作用时间非常短,我们可以假设为一$\delta$函数形式,冲击力对所有冲击取平均值应该为零,而不同时间点的冲击力相乘应该是无关的,所以$F_0(t)$应该满足如下形式
$$\overline{F_0(t)}=0,\overline{F_0(t)F_0(t’)}=c\delta(t-t’)$$
那么我们把布朗运动简化为郎之万方程
$$
\begin{aligned}
&\frac{dv}{dt}=-\gamma v+F(t)\\
&\overline{F(t)}=0\\
&\overline{F(t)F(t’)}=Q\delta(t-t’)
\end{aligned}$$
方程的形式解为
$$v(t)=\int_0^t\exp[-\gamma(t-\tau)]F(\tau)d\tau+v(0)\exp[-\gamma t]$$
考虑足够长的时间,则上式最后一项实际上为零,所以后面我们都只考虑上式右边的第一项,也即考虑足够长的时间
由于碰撞时随机的,显然速度的平均值应当为零,$\overline{v(t)}=0$,但这并不会给我们提供什么有用的信息,所以我们要考虑速度大小的平均值,我们计算
$$
\overline{v(t)v(t’)}
$$
显然考虑极端情况,当$t$和$t’$相隔很远的时候,他们俩的速度之间没有任何关联,所以
$$
\overline{v(t)v(t’)}=\overline{v(t)}\overline{v(t’)}=0
$$
但在一半情况下呢?我们计算
$$
\begin{aligned}
\overline{v(t)v(t’)}&=\overline{\int_0^t\int_0^{t’}\exp[-\gamma(t-\tau)]F(\tau)d\tau\exp[-\gamma(t’-\tau’)]F(\tau’)d\tau’}\\
&=\int_0^t\int_0^{t’}\exp[-\gamma(t-\tau)]\exp[-\gamma(t’-\tau’)]\overline{F(\tau)F(\tau’)}d\tau d\tau’\\
&=Q\int_0^t\exp[-\gamma(t+t’)+2\gamma \tau]d\tau\\
&=\frac{Q}{2\gamma}\left\{\exp[\gamma(t-t’)]-\exp[-\gamma(t+t’)]\right\}
\end{aligned}
$$
任然考虑足够长时间,所以有不同时刻的关联度为
$$\overline{v(t)v(t’)}=\frac{Q}{2\gamma}\exp[\gamma(t-t’)]$$
只与所考虑的时间差有关,且与时间差呈指数下降趋势。
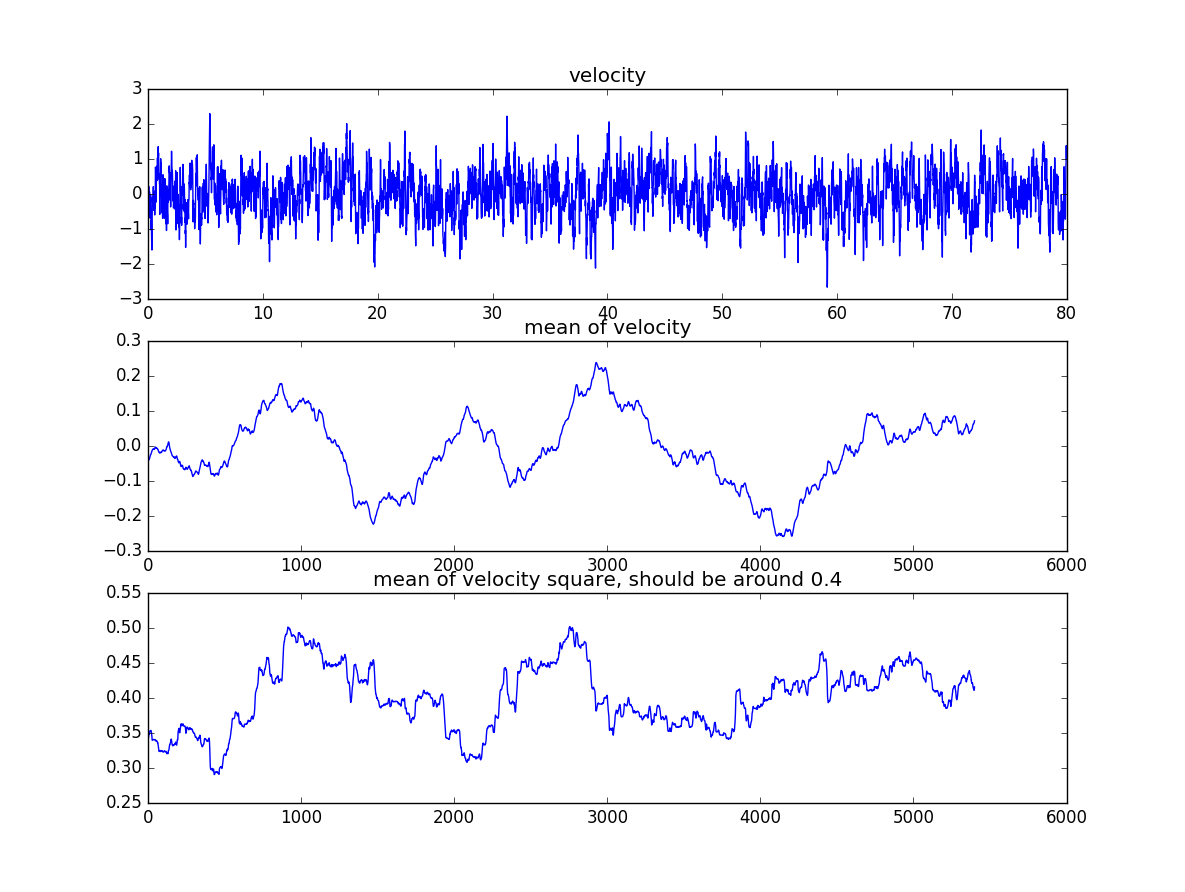
数值模拟
首先我们要进行计算的方程为
$$
\begin{aligned}
\frac{dv}{dt}&=-\gamma v+F(t)\\
&=-\gamma v+\sqrt{Q}N(0,1)
\end{aligned}$$
我们这里设随机力为强度为$\sqrt{Q}$的$0~1$正态分布,显然满足平均值为零,对于关联度我们有
$$\begin{aligned}
\overline{F(t)F(t’)}&=Q\overline{N_t(0,1)N_{t’}(0,1)}\\
&=Q\overline{N^2(0,1)}\delta(t-t’)\\
&=Q\delta(t-t’)
\end{aligned}$$
我们可以解释为,当$t\neq t’$时,两个正态分布无关,那么乘积的平均等于平均的乘积即为零,当$t=t’$时,我们计算的是正态分布平方的平均值,肯定不为零。求解这个随机微分方程(SDE)我们需要用到欧拉-丸山法,具体来讲是要讲方程变形为
$$\begin{aligned}
\frac{dv}{dt}&=-\gamma v+F(t)\\
&=-\gamma v+\sqrt{Q}\frac{dW(t)}{dt}\\
dv&=-\gamma vdt+\sqrt{Q}dW(t)
\end{aligned}$$
而对于$dt$时间段内,$dW(t)$是一个维纳过程,满足$dW=W_j-W_i$服从$N(0,j-i)$的正态分布,即平均值为零,方差为$j-i$
注意,在
python科学计算包中,正态分布函数numpy.random.normal(loc,scale)中,loc为平均值,scale为标准差
所以在我们数值计算的$dt$过程中,$dW$满足的是平均数为$0$,方差为$dt$(标准差为$\sqrt{dt}$)的正态分布。所以我们利用差分的方法可以计算得到
$$v_{i+1}=-\gamma v_i dt+\sqrt{Q}N(0,dt)+v_i$$
有了这个递推公式,代码就很简单了