Adiabatic passage in EIT
No damping
三能级系统哈密顿量为
$$
\begin{aligned}
H&=H_0+H_1\\
&=H_0-ex\cdot E\\
&=H_0-ex\cdot (E_p\cos\phi_p+E_c\cos\phi_c)\\
&=\hbar\omega_{ab}\sigma_{aa}+\hbar\omega_{cb}\sigma_{cc}\\
&+\frac{\hbar}{2}(\Omega_p e^{-i\omega_p t}\sigma_{ab}+\Omega_c e^{-\omega_c t}\sigma_{ac}+H.c.)\\
\end{aligned}$$
此处已选择基态能级为零势能点。选取变换$U=\exp[i\omega_pt\sigma_{aa}+i(\omega_p-\omega_c)t\sigma_{cc}]$,则有新的哈密顿量为
这里用到公式$H’=U H U^\dagger -i\hbar U\partial U^\dagger /\partial t$
$$
\begin{aligned}
H&=-\hbar\Delta_p\sigma_{aa}-\hbar\Delta\sigma_{cc}\\
&+\frac{\hbar}{2}(\Omega_p\sigma_{ab}+\Omega_c\sigma_{ac}+H.c.)
\end{aligned}
$$
其中$\Delta_p=\omega_p-\omega_{ab}$,$\Delta=\omega_p-\omega_c-\omega_{cb}=\Delta_p-(\omega_c-\omega_{ac})=\Delta_p-\Delta_c$
我们取双光子共振条件$\Delta=\Delta_p-\Delta_c=0$,则哈密顿量可写成矩阵形式为
$$
H=-\frac{\hbar}{2}
\begin{bmatrix}
2\Delta_p&-\Omega_p&-\Omega_c\\
-\Omega_p^\dagger&0&0\\
-\Omega_c^\dagger&0&0
\end{bmatrix}$$
系统本征值为$$\lambda_1=0,\lambda_{2,3}=-\frac{\hbar}{2}(\Delta_p\pm\sqrt{\Delta_p^2+|\Omega_c|^2+|\Omega_p|^2})$$
其中本征值为零的态称为暗态,其对应的本征态为
$$\left|Dark\right>=(\Omega_c\left|b\right>-\Omega_p\left|c\right>)/\Omega$$
其中$\Omega=\sqrt{\Omega_p^2+\Omega_c^2}$
为了解共振($\Delta_p=0$)时候演化过程,我们求出运动方程
$$\begin{aligned}
\frac{dc_a}{dt}&=-\frac{i}{2}\left(c_b \Omega_p+c_c \Omega_c\right)\\
\frac{dc_b}{dt}&=-\frac{i}{2}c_a\Omega_p^\dagger\\
\frac{dc_c}{dt}&=-\frac{i}{2}c_a\Omega_c^\dagger\\
\end{aligned}$$
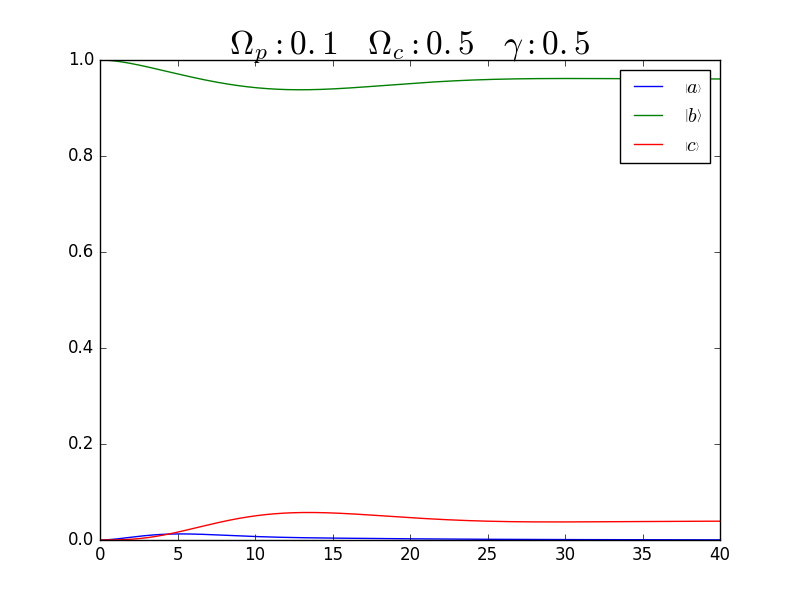
With damping
带damping的运动方程为(共振情形)
$$\begin{aligned}
\frac{d\rho}{dt}=-\frac{i}{\hbar}[H,\rho]-\frac{1}{2}\{\Gamma,\rho\}
\end{aligned}$$
但是对于封闭三能级系统,此方程需要做一些修改,由于是封闭三能级系统,此时我们假设只有激发态会发生damping,所以我们取$\Gamma=\text{diag}[\gamma_1,0,0]$,原来的运动方程做如下修改
$$
\begin{aligned}
\frac{d\rho_{bb}}{dt}&=…+\frac{\gamma_1}{2}\rho_{aa}\\
\frac{d\rho_{cc}}{dt}&=…+\frac{\gamma_1}{2}\rho_{aa}\\
\end{aligned}$$
省略号表示原来的方程,这样就能使的密度矩阵的Trace不随时间改变了。实现代码如下